几何中的最短距离问题

　　近年来安徽的省考中，数量关系考察题目数量相对稳定，为15题，根据统计，其中有一类题型是安徽省特别爱考察的题目，占比在40%左右，几乎占据了数量关系的半壁江山，

考点	2024年	2023年	2022年	2021年	2020年	2019年
排列组合	2	3	1	2	3	1
概率问题	1	1	1	1	2	2
基础应用题	2	3	5	2	2	1
不定方程	0	0	0	1	0	1
几何问题	6	5	6	6	4	4
经济利润问题	1	1	1	1	0	2
行程问题	0	0	0	1	1	1
工程问题	0	0	0	0	0	0
溶液问题	0	0	0	0	0	1
容斥问题	0	0	0	0	0	0
最值问题	0	1	0	0	1	0
数列问题	0	0	1	0	1	0
约数倍数问题	2	0	0	1	0	0
杂题	1	1	0	0	1	2
总题量	15	15	15	15	15	15

　　其中，有一类几何问题格外值得留意，就是关于一条线段同侧两点到这个线段的距离之和最短问题，我们一起来看几道例题。

　　【例1】A点、B点与墙的位置如下图所示，现从A点出发以5米/秒的速度跑向墙，接触到墙后再跑到B点，问最少要多少秒到达B点?

　　A.30

　　B.34

　　C.38

　　D.42

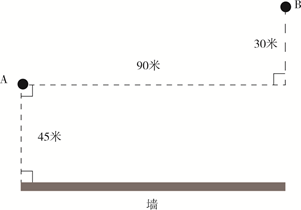
　　【解析】要用最短时间到达B点，在速度一定的情况下，需从A接触到墙后再跑到B点所走的路程最短。如图，由于A和B在墙的同侧，可考虑做其中一个点关于墙的对称点，该对称点与另一个点的连线即为最短路程。这是可以证明的。假设做A点的对称点C，因为C为A的对称点，所以墙上任意一点到A的距离和到C的距离是完全一样的，假设墙上取的点为E点，恒有EA=EC，AE+BE的最小值就是CE+BE的最小值，又因为两点之间直线最短。最短距离为BC。又因为CD=90米，BD=30+45+45=120米，由勾股定理可知最短距离BC=150米，则用时为30秒。

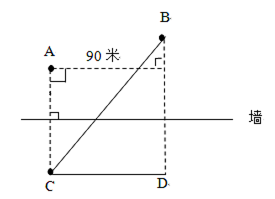
　　这里，最主要的方法是要掌握，两点位于一个线段的同侧时，求两点到线段距离之和的最小值，需要做出一个对称点或者镜像点。然后利用两点之间直线最短，求出所需要的最小值。我们再来看一个更难一些的题目。

　　【例2】如下图所示，某条河流一侧有A、B两家工厂，与河岸的距离分别为4km和5km，且A与B的直线距离为11km。为了处理这两家工厂的污水，需要在距离河岸1km处建造一个污水处理厂，分别铺设排污管道连接A、B两家工厂。假定河岸是一条直线，则排污管道总长最短是：

　　A.12km

　　B.13km

　　C.14km

　　D.15km

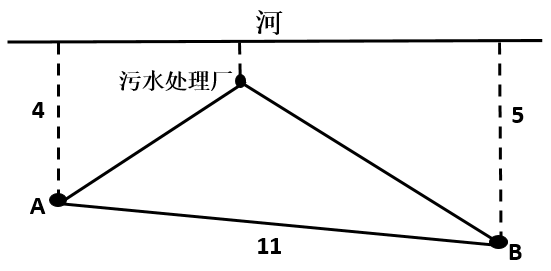
　　【解析】如下图所示，过污水处理厂做河岸的平行线HC，D为A关于HC的对称点，则最短距离为DB，由题污水厂离河1km可得A点距离到HC为HA=HD=3km，B点距离HC等于EH=4km，则DE=7km。由勾股定理可知BE的平方=11*11-1*1=120，所以DB的平方等于7*7+120=169，DB=13km。

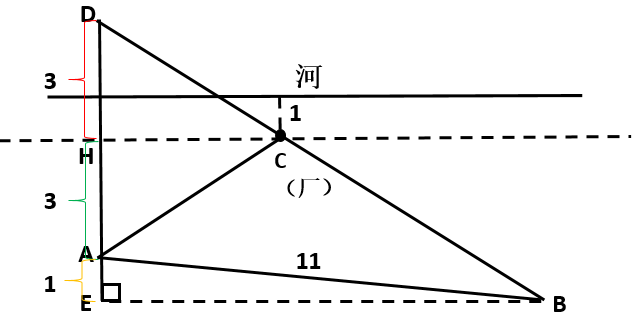
　　这道题相对于上一个题目是要求在河流的平行线上取一个点，所以多了一个步骤，但是核心思想都是相同的。

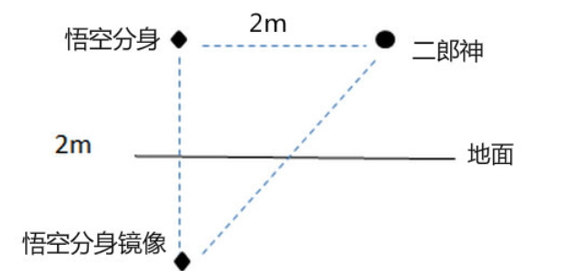
　　又例如【例3】悟空与二郎神在离地面1米的空中决斗，两人相距2米，悟空想用分身直接偷袭二郎神，为了不引起对方的警觉，分身必须在地面反弹一次再进行攻击，则分身到达二郎神的位置所走的最短距离为：

　　【解析】要让分身到达二郎神的距离最短，两点之间连线最短，则应使悟空的分身镜像与二郎神之间的距离最短，如图得到分身的镜像，连线二郎神，距离最短为米。

　　综上所述，这类题目在几何问题中是非常独特的一类题目，跟我们感官上垂直到线段上的距离为最短是有出入的，如何利用镜像和对称去找到最短距离是解开题目的关键所在，掌握这个方法能快速处理此类考题，给考生备考带来便利。